2016年是四川省高考改革承上启下的一年。今年高考,语文、文综、英语听力以及外语小语种(含听力)将使用全国卷,其他科目仍使用四川卷。
考生如何适应全国卷和四川卷?如何才能有针对性地复习备考?
作为指引高考命题的重要依据,《考试说明》是广大师生高考复习备考的”纲领”和风向标。
解读数学:注重基础 提升能力
一、不变——稳定是发展的基石
1.数学知识
今年《考试说明》中的“考试内容”与2015年完全相同,这是广大高三教师的福音。《考试说明》指出,对数学基础知识的考查既要全面又要突出重点,对于支撑学科知识体系的重点内容,要占有较大比例,构成数学试卷的主体。考查应注重学科的内在联系和知识的综合性,不刻意追求知识的覆盖面。从学科的整体高度和思维价值的高度设计问题,在知识网络交汇点设计试题,使对数学基础知识的考查达到必要的深度。怎样理解这段文字呢?且看题型示例中选择题第8题(2014年课标理科Ⅰ卷第6题)。
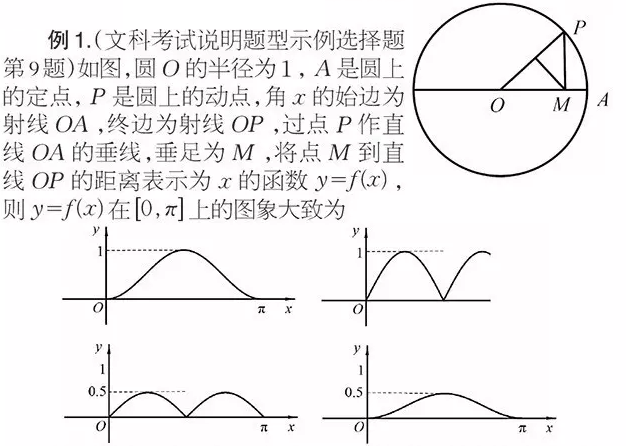
本题考查三角函数的定义、图象等基础知识,同时考查了抽象概括能力和数形结合思想。问题借助几何图形,将教材上三角函数的定义巧妙融合于函数图象中,充分展现了“对基础知识的考查达到必要的深度”和“注重学科的内在联系”。对于同学们复习而言,就是真正理解知识的脉络,形成知识网络。
2.数学能力
相对于2015年的考试说明,我们看到,数学能力的界定,本身变化不大,但是每年的考试总是在解读上出现一定的变化。考试说明指出:数学能力包括五种能力和两个意识,五种能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力;两种意识是指应用意识、创新意识。
我们以运算求解能力为例:中学数学中的运算求解能力是指根据法则、公式进行正确运算、变形和数据处理,能根据要求对数据进行估计和近似计算,它是思维能力和运算技能的结合。运算包括对数字的计算、估值和近似计算,对式子的组合变形与分解变形,对几何图形和几何量的计算求解等,运算能力包括分析运算能力、探究运算方向、选择运算公式、确定运算程序等过程中的思维能力,也包括在实时运算过程中遇到障碍而调整运算的能力。

本题考查函数的性质、导数的运用等基础知识,考查运算求解能力,考查分类与整合思想、创新意识。

本题仅从设问的方式来看,都表达了对运算能力的深刻考查。
对运算能力的考查,数值计算、字符运算和各种式子的变换都是重要内容,其考查要求可概括为“准确、熟练、快捷、合理”。在突出考查算理和算法的同时,对运算的灵活性和实用性也有一定要求,还要求能够恰当运用估算和近似计算。运算能力与考生的知识水平、推理论证能力和心理因素都密切相关。
3.数学方法与数学思想
在中学范围内,数学方法一般不会因为考试年份的改变而发生多大的变化,毕竟常见的诸如换元法、待定系数法、参数法等,这些都是同学们多年学习数学早已熟悉的。同时数学思想的考查也不会单一出现,但考查数学思想的侧重却可能随考试年份而发生改变。
从2015年四川卷来看,“特属与一般”是考查的最为直接的数学思想之一了。
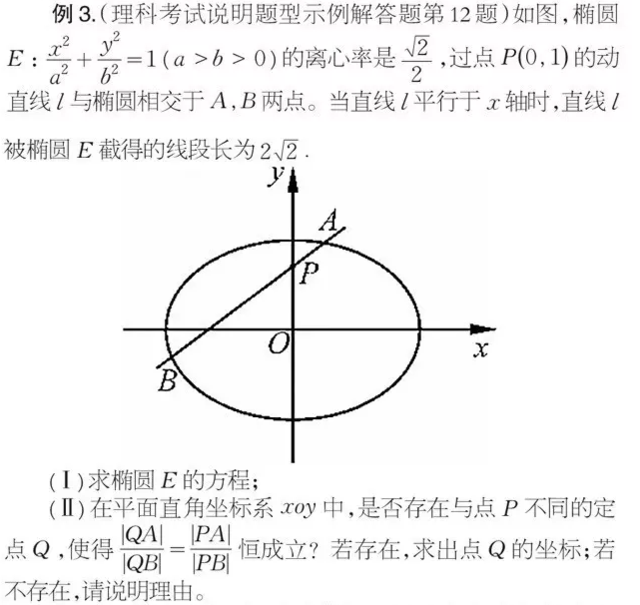
本题主要考查椭圆的标准方程与几何性质、直线方程、直线与椭圆的位置关系等基础知识,考查推理论证能力、运算求解能力,考查数形结合、划归与转化、特殊与一般、分类与整合等数学思想。
其中第二问利用“特殊与一般”的数学思想获得定点Q的坐标是最为优秀的解答方式。如果强行设出点Q的坐标求解,虽然思路自然,而且也有效,但是一点也不简练,考生很可能在考场上陷入运算的泥潭而不能自拔。
二、变化——发展是永恒的
从考试说明中的题型示例来看,一个较大的变化是引入了课标卷中的统计试题,如选择题部分的26、27题,填空题部分的第15题,解答题部分的第3题。

一方面,新引入的题目主要体现为数据处理能力——主要依据统计中的方法对数据进行整理、分析,并解决给定的实际问题,同时也体现了应用意识。
另一方面,这样的变化也表明,概率与统计版块的复习,有必要更加重视统计知识,以更好地切合考试说明中提出的以能力测试为主导,重视考查学生的数学素养。
| 欢迎光临 壹牛家长圈- (http://16jzq.com/bbs/) | Powered by Discuz! X3.2 |